5月5日,美国德克萨斯大学奥斯汀分校宣布联合洛斯阿拉莫斯国家实验室(LANL)和Type One Energy研究团队,成功开发出一款非微扰导向中心模型,大大提高反应堆“漏洞”预测的精度,并将仿星器反应堆的设计效率提升了一个数量级。研究成果已发表在《Physical Review Letters》上,题目为《Nonperturbative Guiding Center Model for Magnetized Plasmas》。

一、研究背景
磁约束核聚变是实现可控核聚变的重要路径,其中仿星器和托卡马克等装置通过强磁场约束高温等离子体。在仿星器设计中,高效约束聚变产生的高能α粒子是维持聚变燃烧和减少壁面材料损伤的关键。
传统微扰导向中心理论通过忽略粒子的快速回旋运动,将粒子运动简化为沿磁场的慢漂移,这为磁约束装置的优化提供了理论基础。但是,该理论依赖小参数ε(ε=ρ₀/L₀,ρ₀为粒子回旋半径,L₀为磁场特征长度尺度)假设。对于高能α粒子,其回旋半径随速度线性增大,导致局部ε
可达15%以上(传统理论适用范围通常要求小于5%),在此情况下,传统理论失效。数值研究表明,在反应堆级仿星器配置中,传统模型与全轨道的α粒子损失率差异可达60%以上,这种差异在准对称设计时更为显著。
二、研究方法
为突破微扰理论的限制,研究团队提出了一种数据驱动的非微扰导向中心模型,核心是从全轨道粒子数据中学习 “非微扰绝热不变量”J,并构建精确的引导中心运动方程。
- 非微扰导心模型的建立:研究者假设存在一个非微扰的U对称性,其无穷小生成元R在ϵ=0时与传统导向中心理论中的旋转变换一致。将相空间中的点用其在导向中心波前面上的交点(足点)来标记,并定义粒子的导向中心为该足点。通过这种方式,将相空间的坐标系转换为足点坐标系,并推导出非微扰导向中心的运动方程。
- 数据驱动学习方法:从全轨道粒子模拟数据中学习非微扰的绝热不变量J。将J表示为一组基函数的线性组合,并通过最小化瑞利商来确定基函数的系数。瑞利商由两个残差项组成,即动态残差(R_dyn²)与不变量残差(R_inv²)。
三、研究成果及结论
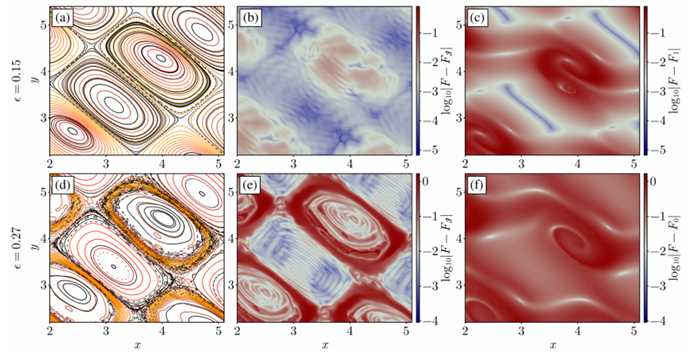
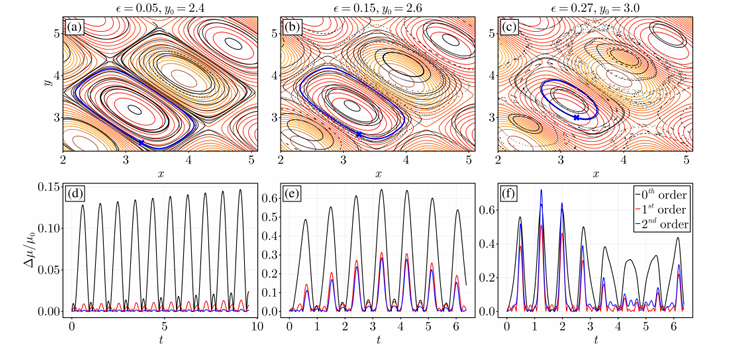
研究结果表明:
- 模型精度显著优于传统导向中心理论,庞加莱截面与全轨道动力学高度吻合
- 相位空间误差较零阶/一阶渐近展开降低多个数量级
- 成功捕捉传统模型遗漏的漂移面偏移等非线性现象
这项研究成功解决了传统理论在强梯度磁场下的失效问题,为高能粒子约束提供了关键解决方案;另外,模型在仿星器α粒子约束和托卡马克逃逸电子问题中展现出显著优势,在保证预测精度的同时可以将计算效率提升一个数量级,也为聚变反应堆设计提供了实用工具。
四、研究局限性
- 模型依赖特定磁场配置的训练数据,一旦磁场结构变化(如仿星器优化中的线圈参数调整),就需重新训练模型,跨磁场的泛化能力仍待提升。
- 模型暂未考虑粒子碰撞、相对论效应(如托卡马克逃逸电子的高能量)和三维磁场的复杂曲率。虽然理论框架支持扩展,但实际应用中需进一步校准,例如引入相对论修正项。
- 模型虽然在训练数据覆盖的ε范围(如15%-27%)内表现优异,但外推至更高值时,其可靠性尚未进行验证。
五、总结
这项研究打破了传统导向中心理论的微扰限制,通过数据驱动方法构建了适用于强梯度磁场的非微扰模型,为高能粒子约束问题提供了关键解决方案。不仅解决了仿星器设计中存在近70年的核心难题,还为托卡马克等其他磁约束装置的优化提供了通用框架。
随着机器学习与等离子体物理的深度融合,未来有望实现从 “基于假设的简化模型” 到 “数据支撑的精确描述” 的范式转变,从而推动磁约束聚变研究迈向实用化阶段。
参考资料:
- https://news.utexas.edu/2025/05/05/university-of-texas-led-team-solves-a-big-problem-for-fusion-energy/
- https://knowridge.com/2025/05/scientists-discover-faster-way-to-fix-key-fusion-energy-problem-after-70-years/
- https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.175101
